
이더리움 공동 창업자인 비탈릭 부테린(Vitalik Buterin)이 이더리움 네트워크의 효율성을 높이기 위해 ‘포세이돈 해시(Poseidon Hash)’ 도입을 고려하고 있다고 밝혔다. 그는 이더리움 연구자들에게 해당 해시 함수의 암호분석 프로그램에 적극 참여할 것을 촉구하며, zk-증명(zero-knowledge proof, ZK) 기술 최적화에 중요한 역할을 할 것이라고 강조했다.
https://m.coinreaders.com/147814
이더리움의 확장성을 늘리기 위한 방법 중 하나로 zk롤업이 한창 개발 중이다. 이더리움의 창시자 비탈릭 부테린은 그 개발의 일환으로 포세이돈 해시라는 것을 도입한다고 발표를 했다. (위 기사 참조)
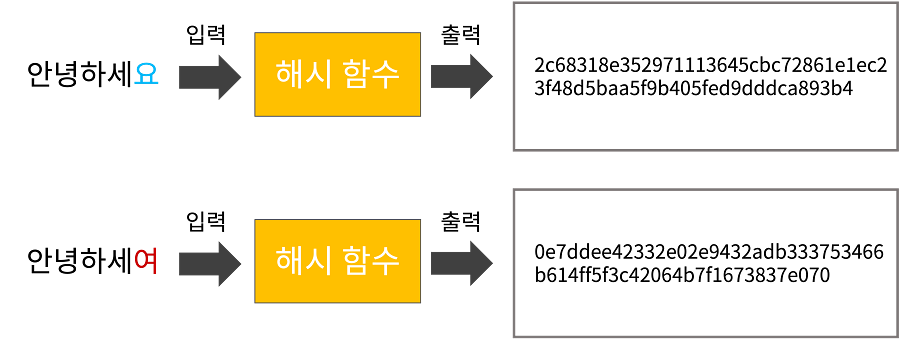
해시 함수(Hash function)는 임의의 길이를 갖는 데이터를 고정된 길이의 데이터로 변환시켜주는 함수로서, 블록체인에서는 해시 함수가 하는 역할은 ‘암호화’로, 해시값 비교를 통해서 위변조 여부를 판별하고, 무결성을 검증하는 데 사용. 대표적인 해시함수는 비트코인의 블록체인에 사용된 SHA-256(Secure Hash Algorithm-256)
SHA-256을 사용하지 않고 포세이돈 해시를 사용하게 된 이유가 무엇이고, 이 포세이돈 해시는 SHA-256 대비 어떤 점이 틀린 지 알아보자.
포세이돈 해시는 영지식 증명(Zero-Knowledge Proof, ZKP) 시스템을 위해 설계된 암호학적 해시 함수입니다. 특히, SNARKs(Succinct Non-Interactive Argument of Knowledge)와 같은 프로토콜에서 효율적으로 작동하도록 설계되었습니다.
1. 포세이돈 해시는 어디에 쓰일까?
✅ ZK-SNARKs / ZK-STARKs
✅ 블록체인(예: 프라이버시 강화, 스마트 컨트랙트)
✅ 메르클 트리(Merkle Tree) 최적화
✅ 이더리움 Layer 2 솔루션(예: zk-Rollup)
2. 왜 기존 해시 함수(SHA-256 등)를 안 쓰고 포세이돈 해시를 쓰나?
✅ ZK 친화적: 기존 해시 함수(SHA-256, Keccak 등)는 ZK 증명에서 연산이 너무 무겁지만, 포세이돈 해시는 연산 비용이 낮음
✅ 빠른 연산 속도: 기존 해시보다 SNARK 증명 생성이 빠름
✅ 모듈러 연산 기반: 기존 해시가 비트 단위 연산을 사용하는 반면, 포세이돈 해시는 유한체(有限體, Finite Field) 연산을 사용하여 ZKP에서 최적화됨
※ 유한체 연산(Finite Field Arithmetic)이란?
유한체(Finite Field, 또는 Galois Field)는 유한한 개수의 원소(숫자)만 가지는 수학적 체(Field)를 의미합니다. 우리가 흔히 사용하는 실수나 정수는 무한한 원소를 가지지만, 유한체는 특정한 개수의 숫자만으로 이루어집니다.
🔹 유한체의 기본 개념
- 원소의 개수가 유한함
- 예를 들어, 정수 집합은 무한하지만,
{0, 1, 2, 3}처럼 원소 개수가 4개인 집합은 유한함.
- 예를 들어, 정수 집합은 무한하지만,
- 덧셈, 뺄셈, 곱셈, 나눗셈이 가능해야 함
- 나눗셈이 가능하다는 것은 0이 아닌 모든 원소에 대해 역원(나눌 수 있는 값)이 존재해야 함.
- GF(p)와 GF(p^n)의 형태가 있음
-
- GF(p): p가 소수(예: 3, 5, 7)일 때, 숫자는
{0, 1, ..., p-1}로 구성됨. - GF(p^n): 더 복잡한 형태로, 보통 암호학에서 많이 사용됨.
- GF(p): p가 소수(예: 3, 5, 7)일 때, 숫자는
🔹 유한체 연산의 예시 (GF(5))
GF(5)는 {0, 1, 2, 3, 4}로 이루어진 유한체입니다.
이 체에서는 **모든 연산을 5로 나눈 나머지(Mod 5)**로 계산합니다.
| 연산 | 결과 |
|---|---|
| 2 + 3 | 0 (5 mod 5) |
| 4 + 4 | 3 (8 mod 5) |
| 3 × 4 | 2 (12 mod 5) |
| 2 ÷ 3 | 4 (2 × 4 ≡ 1 mod 5) |
즉, 모든 계산이 특정한 유한한 범위 안에서 돌아감.
🔹 유한체 연산이 왜 중요할까?
- 암호학 & 블록체인에서 필수
- 유한체 연산은 RSA, ECC(타원 곡선 암호), 포세이돈 해시 등 암호학적 알고리즘에서 중요한 역할을 함.
- 특히 ZK-SNARKs, ZK-STARKs 같은 영지식 증명에서 많이 사용됨.
- 빠르고 효율적인 연산 가능
- 무한한 실수 연산보다 컴퓨터에서 처리하기 쉬움 → 계산 속도 향상
- ZK 증명에서 해시 연산을 빠르게 만들기 위해 활용됨
- 충돌 없는 해시 설계 가능
-
- 유한체를 이용한 해시 함수는 기존 SHA-256보다 ZKP에서 증명 생성 속도가 빠름.
🔹 포세이돈 해시와 유한체 연산
포세이돈 해시는 기존 해시 함수(SHA-256, Keccak)와 다르게 유한체 연산을 기반으로 동작합니다.
즉, 숫자를 비트 단위 연산이 아닌 수학적 연산(유한체 덧셈, 곱셈, 역원 계산 등)으로 변환하여 연산함.
- SHA-256 → 비트 단위 XOR, Shift, AND, OR 연산
- 포세이돈 해시 → 유한체 덧셈, 곱셈, 행렬 연산 등 사용
이렇게 하면 ZK 증명 생성 시간이 크게 단축되므로 zk-Rollup, Layer 2 블록체인 등에서 효과적!
3. 포세이돈 해시의 원리 (간단 버전)
SHA-256 같은 해시는 비트(bit) 연산 기반이지만, 포세이돈 해시는 수학적 함수(유한체 연산과 행렬 연산)를 기반으로 동작합니다.
- 입력 값(X)을 유한체(Field) 내 숫자로 변환
- 특정 행렬(Matrix)과 비선형 함수(Non-linear function, 즉 S-box)를 적용하여 변형
- 여러 라운드(Rounds)를 거치면서 값을 섞음
- 최종적으로 해시 값 출력
4. 포세이돈 해시의 장점
✅ ZK 증명에 최적화 → SNARK 및 STARK에서 연산이 빠름
✅ 블록체인과 궁합이 좋음 → zk-Rollup, 메르클 트리 등에서 활용
✅ 암호학적으로 안전 → 기존 해시보다 특정 환경에서 더 강력한 보안 제공
📌 정리
포세이돈 해시는 영지식 증명(ZKP)에 최적화된 해시 함수로, 기존 SHA-256이나 Keccak보다 ZK 환경에서 빠르고 효율적인 연산이 가능하도록 설계된 해시 함수입니다.
블록체인의 프라이버시 기술(ZK-Rollups, zkEVM 등)에서 매우 중요한 역할을 하며, 앞으로 더욱 활용될 가능성이 높습니다.


